• 数学
• 决策树
  • 剪枝理解

决策树就是一个if-then规则的集合:

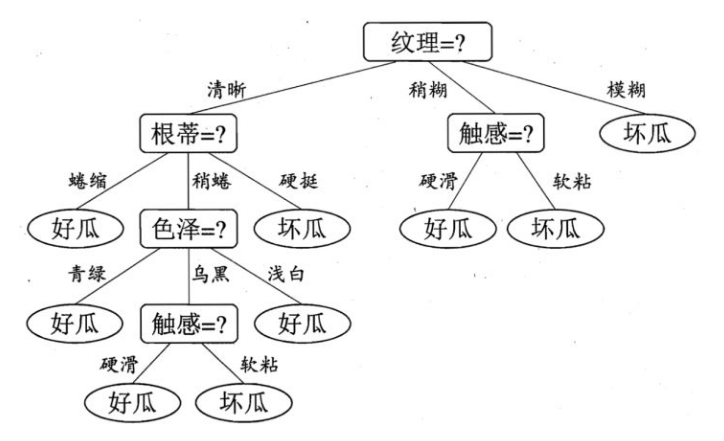
如果对决策树建模是核心.对应到上图，为何先要看纹理，再看根蒂?,多少才算是纹理清晰？

数学

信息熵

条件熵

最小二乘

决策树

从众多可能的if-else决策树中，选出与训练数据最贴近，同时又有最好的泛化能力(预测能力,不过拟合)的那个

• ID3

采取信息增益这个量来作为纯度的度量,引入特征 a 使得整体不确定的减少，选择减少最大的那个特征作为分裂特征.

原来有那么多不确定度(信息熵)，引入了新的条件后得到新不确定度，即信息熵(条件熵),总的不确定度肯定是减少了，两者的差就是信息的增益

\[g(D,a) = H(D) - H(D|a)\]

参考 1

参考 2

参考 3

• C4.5

ID3的缺陷在于对信息增益准则其实是对可取值数目较多的属性有所偏好.可能不具备很好的泛化能力.

信息增益率来选择最优划分属性.

信息增益率也不是越大越好，其对可取类别数目较少的特征有所偏好，分母越小，值越大。

于是 C4.5 算法不直接选择增益率最大的候选划分属性，候选划分属性中找出信息增益高于平均水平的属性（这样保证了大部分好的的特征），再从中选择增益率最高的（又保证了不会出现编号特征这种极端的情况

• CART(Classification And Regression Tree)

分类回归树,可做回归树也可做分类数.

全是二叉树.

回归树选取划分后平方误差最小化的属性进行划分. 分类树选取划分后基尼指数最小的属性进行划分.

具体是针对每一个特征 j，在该特征的特征集里，选择 gini_D_a 最小的值 a，比较所有特征的 a,选最小的特征对应的 a 作为本次分裂的切分点.

停止条件类似 ID3

剪枝理解

参考

这个怕是决策树里最难理解的部分了.

所谓剪枝,即去掉子树(interanl + leaf node)或者单纯的叶结点(leaf),将父结点(原来是 internal 结点),变为新的叶结点.变的方式就是将子树或者叶结点里的样本来统计属于某一个类即可变成叶结点。

id3,c4.5 的剪枝算法和 cart 的剪枝算法是不同的

• id3,c4.5

a 是固定的，对于任意子树 T,因为叶节点是固定的，上面的式子可算。

于是从树的底层的叶结点开始回缩叶结点，也就是剪的动作,剪后的损失函数如果变小，则真真的剪掉，形成新的子树，再次从底层递归回缩，重复计算…直到不能继续，于是得到损失函数最小的树

• cart cart 最大的不同就是 a 不是确定值，而是假定从 0->无穷，对应的 n 个 a 的区间，每个区间都有一个最佳的树， 如果得到最优子树?

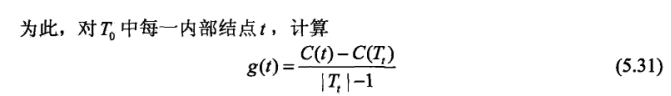
这个式子计算 min，最小的 t 对应的 T 应该被剪掉，之后得到的即区间的最佳的树。

假设把区间分为 10 个，(10 个 a)，对应到可以算出 10 个最佳树，然后再交叉验证，确定最佳的决策树