Machine learning 决策数算法实现心得
前言
做算法的基本提升方法,纯自我总结…没有参考,无指导意义。
- 读懂算法
- 实现基本流程
- 调优,如性能优化,边界错误处理,尝更多数据集检验模型,交叉验证等
- 加花,如结果可视化,尝试比较变种算法效果
- 尝试用现成成熟框架 ts,sklearn,kaggle,等等
- 尝试 c 艹..
决策树
算法本身不算难,主要当然是参考统计学习方法了.
实现核心即: numpy + 递归生成节点 +节点定义及可视化。中间有几个 python 技巧,如是而已。
- 条件概率计算的实现
通过特定的列(即 x)的值,来筛选样本(y),计算条件概率必备;
unique很好用;
def counts_by_feature_and_class(data,ft,ft_val,cls=None):
#total是个[True False]矩阵,表示满足条件的行是否存在
if cls == None :
total = data[:,ft]==ft_val
else:
# logical_and可以基于多个列条件筛选,得到新的[True False],作为数据统计
total = np.logical_and(data[:,ft]==ft_val,\
data[:,(data.shape[1]-1)]==cls )
ret = np.sum (total == True)
# print('ft=',ft,'ft_val=',ft_val,'cls=',cls,'counts',ret)
#不能算log2(0),用极小的值代替0
if ret == 0:ret = 0.00001
return ret
- skip_feature
划分子集时,跳过样本的特征列,而不是用 data_set 删掉特征后的拷贝
feature_vars=[]
feature_counts=[]
for i in range(feature_nums):
if skip_features != None and i in skip_features:
print('skip',i)
continue
var,counts = np.unique(data_set[:,i],return_counts=True)
feature_vars.append(var)
feature_counts.append(counts)
- 划分子集:
d[d[:,real_idx] == i,:]
这语法比较好:取 d 中 real_idx 列等于 i 的哪些行.
如果需要多个列多为条件,用np.logical_and生成TrueFalse矩阵同样去筛选即可
children=[]
child_feature_val=[]
for i in full_fts[real_idx]:
children.append(d[d[:,real_idx] == i,:])
child_feature_val.append(i)
- 节点定义
一个 dict,创建时想怎么放就怎么放.用了 1 个value反查key的技巧为了画图用。
class dt_node(object):
def __init__(self,**kwds):
self.node = kwds
# print('new node',self.node)
feature = {}
feature["leaf"] = -1
feature["age"] = 0
feature["job"] = 1
feature["house"] = 2
feature["bank"] = 3
feature["class"] = 4
# 根据value 反查key
rever_dict = {v:k for k,v in feature.items()}
# print('node',rever_dict[kwds['idx']])
self.name = rever_dict[kwds['idx']]
node_lists.append(self)
创建时:
dt_node(idx=-1,property='leaf',father=father,val=vals[0],ft_val=feature_val[j])
node = dt_node(idx=real_idx,property='internal',father=father,val=-1,ft_val=feature_val[j])
- 多叉数可视化
用了 pydoyplus,蛮简单的 安装一下:
sudo apt-get install graphviz
conda install pydotplus
#可视化决策树
# sudo apt-get install graphviz
# conda install pydotplus
g = pydotplus.Dot( graph_type='digraph')
i = 0;
for item in node_lists:
print('name:',item.name,'node=',item.node)
#不同node强制用不同的名字
node_name = item.name
if node_name == 'leaf' and item.node['val'] != -1:
node_name = "leaf"+str(i)+"\n"+str(item.node['val'])
print(node_name)
i+=1
node = pydotplus.Node(node_name)
if item.node['property'] == 'internal':
node.set('shape','diamond')
else:
node.set('shape','box')
father_node_name = item.node['father']
if father_node_name != 'root':
father_node_name = item.node['father'].name
father_node = pydotplus.Node(father_node_name)
edge = pydotplus.Edge(father_node_name,node_name)
if 'ft_val' in list(item.node.keys()):
edge.set('label',item.node['ft_val'])
# if item.node['val'] == 1:
# edge.set('label','yes')
# elif item.node['val'] == 0:
# edge.set('label','no')
g.add_node(node)
g.add_node(father_node)
g.add_edge(edge)
g.write("dt-tree.png", format='png')
import os
os.system("eog dt-tree.png")
- 递归结束条件
剩下样本全部属于某类时,leaf node 并做类标记;
特征集为空,(skip_feature 为满),剩下数据直接根据剩余最大的类作为类标记;
如果计算 g_D_A 后,发现信息增量(id3)已经很小了(0.1),同上。
最终效果:
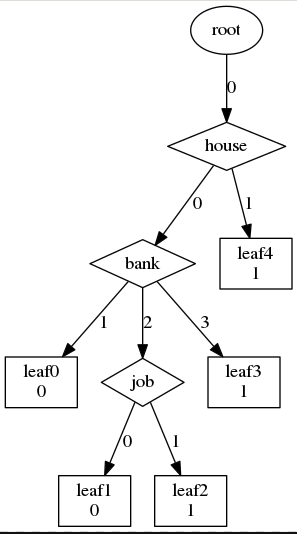
尝试修改样本,然后生成不同的决策树,真的可以解释,蛮有意思的
- 对剪枝的理解
分的太细容易过拟合.
一种是生成数前就是通过提前分析数据确定分支数和深度;
一种是生成树后,通过测试集反馈的错误再裁剪分支,合并子树等,将根节点或者父节点作为新的叶节点,从而简化树的模型
kaggle 的 titannic data
经过对数据的预处理:
不要 id 类,不要有缺失的数据,最后得到的特征为Sex,Pclass,parch,sibsp,embark,分别是性别,几等票,有无亲人,有无兄弟,上岸地点等.
最后得出这么个结论:
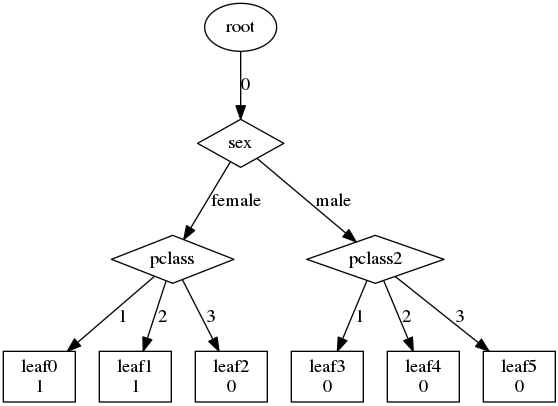
总的就是说中产阶级或者富家的女人的存活率高…感觉还挺对的?…
然后对比一篇非常详细的jupyter note
算是对 data anaysis 的入门的好文章,
- pandas 真的很方便
- 预处理数据的技术及思路
- 数据预分析,看特征的相关系数,比较 title 和 name 特征的差异等等
- 交叉验证的思路来确定最佳的 tree depth;
- sklearn 调用 disicsion tree;
- tree 的画图
对比自己的做法:
- 数据裁剪
- 调用自己的 tree 函数
- 画图 (基于 node 和 pydotplus)

