Machine learning Logistic regregssion
基本理解
linear regression 用于回归,而 logistic regression 用于分类,不要被迷惑.先讲 2 元的,再推广到多元的分类。
预测函数
预测函数为在已经观测样本和参数下,y=1 的条件概率密度函数:
\[h_{\theta}(x^{(i)})=\frac{1}{1+e^{-\theta^{T}x^{(i)}}}=P(y^{(i)}=1|x^{(i)},\theta)\]概率越大的结果则为相应的分类。
代价函数
单个样本的代价函数定义:
\[J(\theta )= -log(h_{\theta}(x))) ,when\ y= 1;\] \[J(\theta )= -log(1-h_{\theta}(x))) ,when\ y= 0;\]写成 1 个公式即:
\[J(\theta) = -y*log(h_{\theta}(x))) -(1-y)*log(1-h_{\theta}(x)))\]整个代价函数为:
\[J(\theta) = -\frac{1}{m}\sum_{i=1}^{m}\left ( y*log(h_{\theta}(x^{(i)}))) +(1-y^{(i)})*log(1-h_{\theta}(x^{(i)}))) \right )\]vectorazation 后(fminunc 写 costfunction 时要用),即:
\[J(\theta) = -\frac{1}{m}\left ( log(g(X^{T}\theta)) + (1-y^{(i)})^{T}* log(g(1-X^{T}\theta)) \right )\]如何理解代价函数?
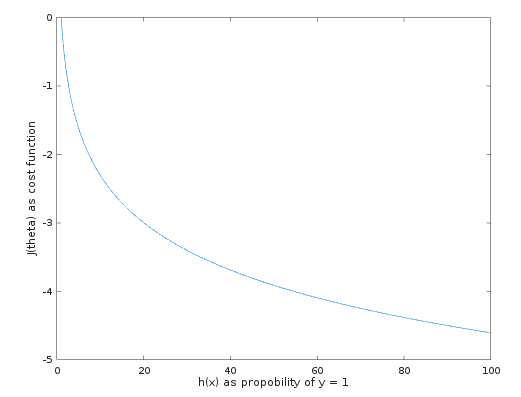
$h(\theta)$表示参数$\theta$,和观测样本 x 下,标签 y=1 的概率,概率越大,代价函数越小,惩罚越小,欧负责增加该样本对整体模型的惩罚,这就是 LR 代价函数的内涵。
梯度下降法求解
问题描述为:
\[arg\ \underset{\ \theta}minJ(\theta), which\ J(\theta) = -\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}*log(h_{\theta}(x^{(i)}))) +(1-y^{(i)})*log(1-h_{\theta}(x^{(i)}))))\]梯度下降法求解为:
\[\theta_{j} = \theta_{j} - {\alpha}\frac{\partial J(\theta)}{\partial \theta_{j}}\]最终求解为:
\[\theta_{j} =\theta_{j} - \frac{\alpha}{m}\sum_{i=1}^{m}\left ( h_{\theta}(x^{(i)} - y^{(i)}) \right )\cdot x^{(i)}_{j}\]vectorazation 后:
\[\theta = \theta - \frac{\alpha}{m}X^{T}(g(X\theta)-y)\]最终求解的形式和线性回归非常像,只不过用$g(X\theta)$代替了$X\theta$
优化方法求解
面对巨多的特征时,如何让计算更加快?
Ng 提到的是Conjugate Gradient descent,BFGS,L-BFGS.,可以自动学习$\alpha$,让 convergence 更快.
octave 里有个 fminunc 直接使用
定义 1 个 costFunction,jVal,gradient 的形式决定了使用什么算法
function [jVal,gradient] = costFunction(theta)
jVal=xxx;
gradient = xxx;
end;
调用fminunc,计算非约束的优化问题,底层可能是 GD,也可能是上面提到的优化算法。
option = optimset('GradObj','on','MaxIter',100);
initTheta = zeros(2,1);
[thetaVal,functionVal,exitFlag]=fminunc(@costFunction,initTheta,option,);
多元线性回归
一对多的思想,如三元分类,变成 3 个 2 元分类的问题.
哪个概率大,哪个就是预测值.
问题来了,对于 fminunc 怎么计算多元特征的 cost function? 难道针对每个分类,都用 1 次 fminunc 算出一个$\theta$,计算预测样本对应的的$h_{\theta}(x)$,这样的值要计算 n 回,然后取最大值的那个作为预测的标准?
多元的例子
实践下,造个数据集:
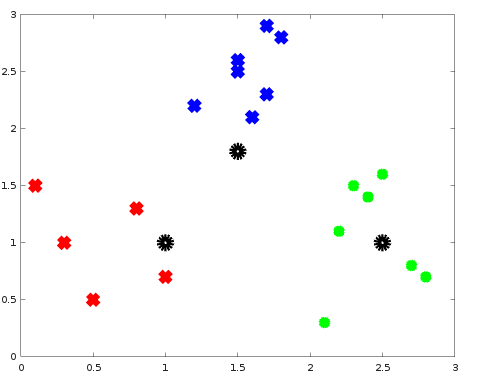
octave 代码如下:
clc;close all; clear all;
% get train
load 'train.txt';
%重新组合的样本集便于画图
train_c = [];
%找到所有标签
labels = unique(train(:,end))';
%存储不同标签的样本的数量
set_size = [];
n = 1
for i = labels
%遍历每个样本, r为i对应的样本行号
[r,c] = find(train(:,end)==i);
set_size(n) = length(r);
train_c= [train_c;train(r,:)];
n = n+1
end;
figure;
p1 = set_size(1);
p2 = set_size(1)+set_size(2);
p3 = sum(set_size);
range1=1:p1;
range2=p1+1:p2;
range3=p2+1:p3;
xlabel('feature 1');
ylabel('feature 2');
plot(train_c(range1,1),train_c(range1,2),'rx','markersize', 10,'linewidth',8);
hold on;
plot(train_c(range2,1),train_c(range2,2),'bx','markersize', 10,'linewidth',8);
hold on;
plot(train_c(range3,1),train_c(range3,2),'g*','markersize', 10,'linewidth',8);
%定义costFunction
function [jVal,gradi] = costFunction(theta,X,y)
m = size(X,1);
% without regulazation
jVal = -(1/(m)) * sum ((y'*log(sigmoid_e(X*theta))+(1-y)'* log(1 - sigmoid_e(X*theta))));
gradi = X' * (sigmoid_e(X*theta) - y ) / m ;
% with regulazation
lambda = 0.9;
new_theta = [0; theta(2:end)];
jVal = -(1/(m)) * sum ((y'*log(sigmoid_e(X*theta))+(1-y)'* log(1 - sigmoid_e(X*theta))));
(lambda/(2*m)) * theta(2:end)'* theta(2:end);
gradi = X' * (sigmoid_e(X*theta) - y ) / m + lambda /m * new_theta ;
end
function [thetaVal, functionVal, exitFlag] = calTheta(feature,data)
%遍历每个样本, r为i对应的样本行号
[r1,c] = find(data(:,3)==feature);
[r2,c] = find(data(:,3)!=feature);
train_c_binary = data;
train_c_binary(r1,3) = 1;
train_c_binary(r2,3) = 0;
train_c_binary = [ones(size(train_c_binary,1),1) train_c_binary];
X = train_c_binary(:,1:3);
y = train_c_binary(:,4);
m = size(train_c_binary,1);
initTheta = zeros(3,1);
option = optimset('GradObj','on','MaxIter',400);
[thetaVal,functionVal,exitFlag]=fminunc(@(t)costFunction(t,X,y),initTheta,option);
end
% only one
thetas = zeros(3,3);
n = 1;
for i=labels
[t, f, flag] = calTheta(labels(n),train);
labels(n)
t
f
flag
thetas(:,n) = t;
n = n+1;
end
function [val,class] = predict(x, thetas)
vals = sigmoid_e(thetas'*x);
vals
[val,class] = max(vals)
end
%thetas = zeros(3,1);
%n = 1;
%[t, f, flag] = calTheta(1,train);
%t
%f
%flag
%thetas(:,1) = t;
%function [val,class] = predict(x, thetas)
%vals = sigmoid_e(thetas'*x);
%vals
%if vals > 0.5 class = 1; end
%if vals < 0.5 class = 0; end
%end
while(1)
x = input("input a x:\n");
x = [1, x]
hold on;
plot(x(2),x(3),'ko','linewidth',8,'markersize',10);
[val,class] = predict(x',thetas);
x
disp('class')
class
end
比较关键的就是 costFunction 里的 J_theta 和梯度的计算,一定主要是vectorazation让计算变的更加简洁。
另外刚开始数据集没造好,导致 fminunc 报错,吸取教训。
发现自己还是超前了一点点 ng 的课程,week4 的手写识别,(5000 个样本,每个样本 20x20 pixel)完全可以用多元 logistic regression 来实现了,注意加上正则化就好.

