By

引言

算法模型也建立了，训练是对的，但是效果不好,怎么办?

  • 交叉验证

  • 分析评估算法的性能

  • Machine learning diagnostic(机器学习诊断法)

交叉验证

参考

  • 简单交叉验证 :

选 7-3 分 训练/测试,无验证集,有可能的多个模型:

线性回归:选测试误差最小的那次参数.

分类问题:选择误分率最低的参数.

  • 带验证集的交叉验证

6-2-2 分 分为训练，交叉验证集合/测试集

交叉验证集用来确定模型选择的一些参数，如隐层个数，多项式个数等等,正则化的 lambda 等…

就是把原测试集再分为验证集和测试集，验证集用来选择模型参数，而测试集就是纯粹的测试集，只使用一次,不参与参数/模型选择，仅评估已有模型的好坏。如果测试集也参与模型选择，很可能仍未更好的解决过拟合的情况，就是简单交叉验证的缺点。

  • k 折交叉验证

如 k=10.数据分 10 坨，每次用 9 坨训练，另外 1 坨测试，每个模型做 10 次，取均值误差率最小的模型.

bias and variance 评价不同模型

用 Jtrain 和 Jcv 为纵坐标，其他变量(正则化参数$\lambda$，样本数目 m,二次特征个数 d 等等)，可以分析变量合理的取值，以及当前学习算法的基本状况。

2 次特征个数 d 的情况:

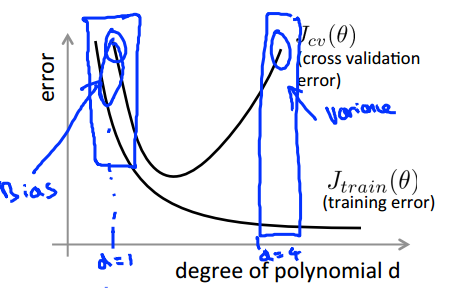
2018-04-19-11-40-47

正则化参数:

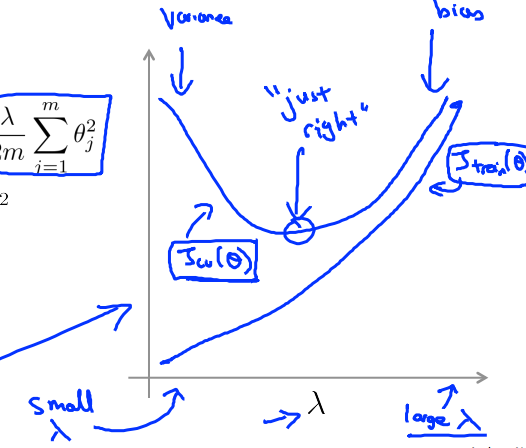
2018-04-19-11-42-39

样本数 m 的分析,正常情况:

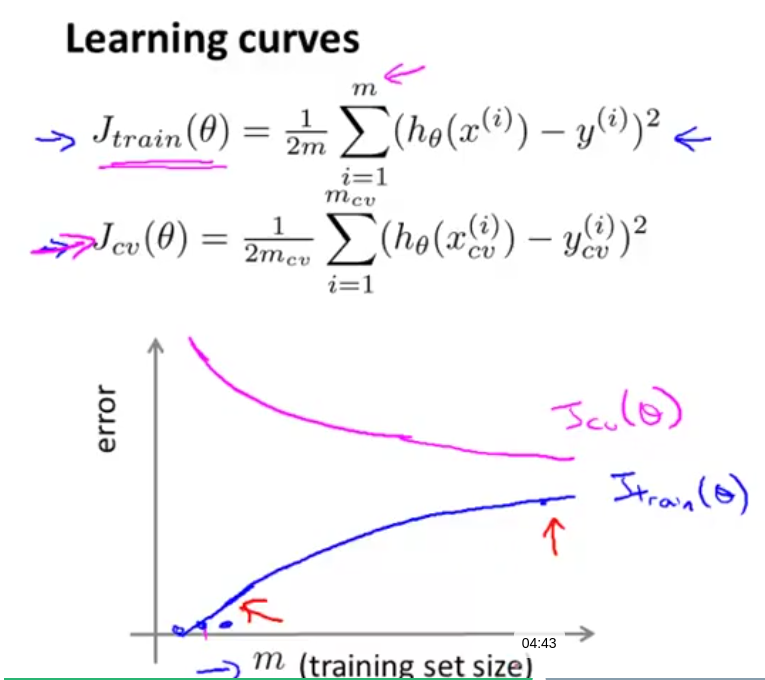
2018-04-19-10-56-47

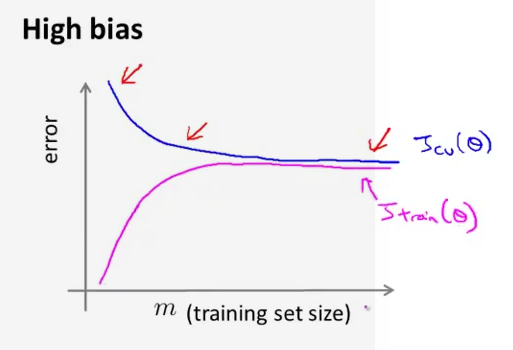
  • high bias

Low training set size: causes Jtrain(Θ) to be low and JCV(Θ) to be high.

Large training set size: causes both Jtrain(Θ) and JCV(Θ) to be high with Jtrain(Θ)≈JCV(Θ).

high bias 时，增加样本容量 m 不会改善性能，减少误差;

2018-04-19-10-59-29

  • high variance

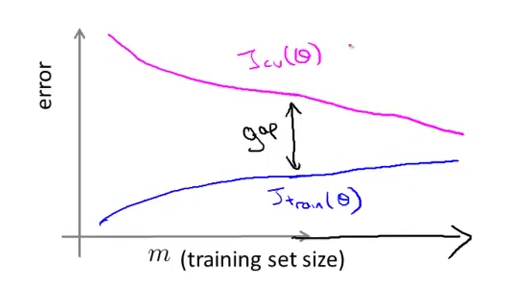
2018-04-19-11-07-57

Low training set size: Jtrain(Θ) will be low and JCV(Θ) will be high.

Large training set size: Jtrain(Θ) increases with training set size and JCV(Θ) continues to decrease without leveling off. Also, Jtrain(Θ) < JCV(Θ) but the difference between them remains significant.

high varience 时，增加样本容量 m 也许可以改善性能;

what you should do next

2018-04-19-11-15-57

  1. 要不要增加样本？如果是 high bias，按上面分析，没有必要，high variance 可以尝试;
  2. 减少特征数目?同样的，如果是 high bias 欠拟合，要增加特征而不是减少，所以在 high variance 可以尝试减少特征，防止过拟合。
  3. 增加额外特征，和上面相反，适应 high bias;
  4. 增加额外多项式特征，说明是 high bias 了，
  5. 太大的$\lambda$导致参数必须很小，意味着 high bias
  6. 过小的$\lambda$意味着没有起到正则化的惩罚效果，为过拟合，(high variance)

反过来说：

欠拟合时：增加额外特征，包括多项式特征，减少正则惩罚参数;

过拟合时：尝试增加样本，减少不必要特征，，增加正则惩罚参数;

对 bpnn 来说，小的网络容易欠拟合，计算量小;大的网络容易过拟合，计算量大.

ex5 的作业

先用一个简单模型拟合看看，从 jtrain 和 jerror 随样本变化(即学习曲线)，看出$1\theta_{0}+x_{1}\theta_{1}$的简单模型是欠拟合的.

于是增加 poly 的多项式,(lamba=0)即把特征增加到了 p*2 个:

   X_poly(i, :) = [X(i) X(i).^2 X(i).^3 ...  X(i).^p];

遍历$\lambda$找到最佳的正则化值…

(我觉得应该先看 p 取多少合适，先确定模型，再来确定正则化参数…)

ok,假定当前的 p 是合理的，选择$\lambda$怎么选？当然是用 Jcv 最小的那个$\lambda$.

{0; 0:001; 0:003; 0:01; 0:03; 0:1; 0:3; 1; 3; 10}

最后得到 Jtrain 和 Jcv 曲线

2018-04-19-15-44-51

误差分析

The recommended approach to solving machine learning problems is to:

Start with a simple algorithm, implement it quickly, and test it early on your cross validation data. Plot learning curves to decide if more data, more features, etc. are likely to help. Manually examine the errors on examples in the cross validation set and try to spot a trend where most of the errors were made.

手动检查算法犯的错误(Jcv 中的错误分类), 用数据来描述再添加某些/去掉某些特征后的错误程度(error 3.3% for ex),

偏斜类

某个分类正类，负类的比值非常小(比如 0.5%为正，其余均为负),如过某个模型最终训练后，在测误集合上的误差为 1%,看上去还不错，实际比真实还要高,所以用分类误差来评估模型效果也会有问题,这样的分类叫偏斜类问题.

查准率/召回率/F 值

推荐系统评测指标

$h_{\theta}(x) >= threhold ,predict y = 1$ ,threhold 为置信区间，可以用 F 值的大小来确定何时的置信区间

最后的例子