• 和常规 SVM 理解不同
• kernel
• 参数选择
• K 分类 SVM
• 如何选择 ls 和 svm 算法
• 垃圾邮件分类的特征工程

和常规 SVM 理解不同

看的教材也好，参考文章也罢，都是从最大化间隔 $\frac{2}{||\omega||^{2}}$ 出发，然后提出优化目标，一通复杂的数学后得出了:

\[\underset{w,b}{min}\sum_{i=1}^{m}max(0,1-y_{i}(\omega^{T}*\phi(x_{i})+b) + \frac{2}{\lambda}||\omega^{2}||)\]

Ng 的思路刚好相反，从 logistic 和 hingo 铰链函数的相似性出发，并交换了正则化(由$\lambda$到$C$,$C=1/\lambda$),并在约束条件下，可以得到等价的优化目标:

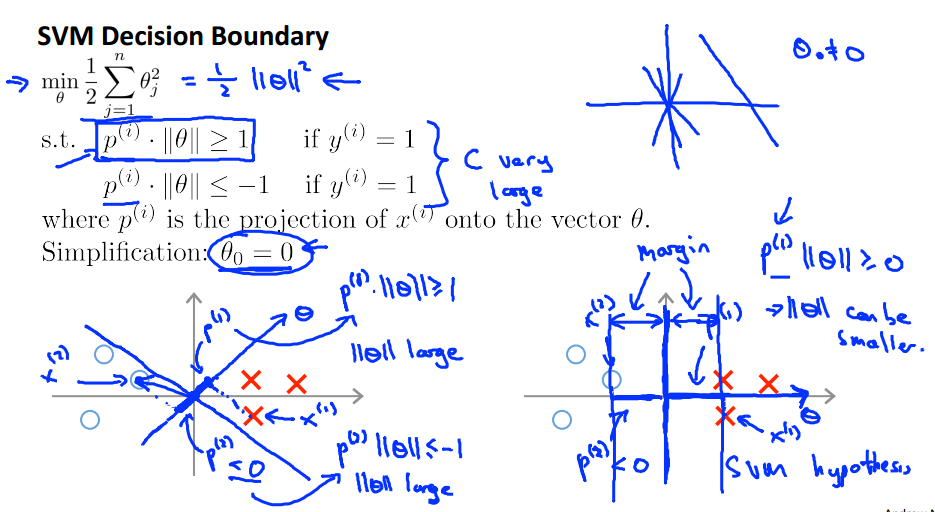
\[\underset{\theta}{min}\sum_{j=1}^{m}\theta_{j}^{2} \\ st. x^{T}\theta_{i} \geq 1,when \ y_{i}&=1\ and \ x^{T}\theta_{i} \leq 1,when \ y_{i}=0 \end{align*}\]

然后从内积($x^{T}\theta_{i}$)和欧式距离$sum_{j=1}^{m}\theta_{j}^{2}$的物理意义，即来直观理解SVM是如何选择决策边界的. $$

kernel

kernel 的理解，比如高斯核函数:

\[k(x^{i},x^{j}) =exp(\frac{||x^{i}-x^{j}||}{2/\sigma^{2}})\]

表示 xi,xj 的相似程度，相同为 1,越不同，越接近 0,也就是对一个原来样本的一个点 xi，通过 kernel 函数映射了 n 维一个向量，每个向量的长度为样本的总长度 n,(由原特征空间维度 m 变成样本空间长度 n)

\[f=[f1,f2,...fn],where\ fi= exp(\frac{||x^{i}-x^{j}||}{2/\sigma^{2}})\]

另外 n 是可以取无穷维的，这就是维度映射的概念.

从数学公式角度，exp 函数可以用泰勒公式展开，也就是背后的数学原理.

线性核就是没有使用核函数的结果.

参数选择

C 越大，$\lambda$越小，过拟合(high variance)

C 越小，$\lambda$越大，欠拟合(high bias)

$\sigma$越小，f 变化越陡峭，过拟合(high variance)

$\sigma$越大，f 变化越平缓，欠拟合(high bias)

K 分类 SVM

和 logistic regression 相似，用 onevsall 的思想，把 1 个多分类，变成 n 个 2 元分类，保留每次正分类的结果(概率)，最后比较谁最大就好了。

如何选择 ls 和 svm 算法

样本数为 m，特征维度为 n

n » m 时，lr or svm without kernel;

n 很小，m>n,一般般大，svm with gaussian kernel better;

m»n，lr or svm without kernel;

垃圾邮件分类的特征工程

email 如何做特征工程?

• 去掉异常符号标点;
• 将变化的网址，价格等用不变的量表示如 emailaddr dollar;
• 单词 stem 化 如 discouts discounted discounting 统一为 discount;

最后的 test 里选取频率最高的(比如 2000)个单词作为特征,然后将每个 email 样本转化为 [0 1 0 0 1 0 0 1…]这样的向量。

gaussian kernel 处理之。