Machine learning Anmonly detection
数学补充
随机变量
随机变量的基本概念,首先它是一个函数,那就有取值范围,其值域是某个取值空间(事件空间)的子集(或本身),而这个取值空间,就是一个随机现象的所有可能的事件结果。而它的自变量就是某次具体的随机事件.
因为是数学嘛,(符号,数值化!~),这个取值空间Ω中每一个点,也就是每个基本事件都有实轴上的点与之对应.(一次抛硬币的结果,X=1表示正面,X=0反面),因此随机变量也是一个实值(1,0,…)的函数。
那如何描述多个事件的这种子集呢,比如普通函数,有$a \leq y \leq b$ 这样的限定方式,那么也可以用$X(\omega) \leq x$ 这样来描述某些随机事件的集合.
再来理解随机变量完整的定义: 对任意实数x,{ω:X(ω)<=x} ∈ F的实值函数为随机变量。F可以为事件全体空间,ω代表一次具体事件,x是值域的取值限定,X(ω)即是随机变量这个函数.
还是有点抽象,举1个具体栗子:
连续4次抛硬币的结果为一次随机实验,是一个样本空间,取值空间为{正正正正,反反反反,正反反反,…}共有16种.比如定义1个随机事件为出现2正2反(即ω,没有规定正反谁先出现),这就是一个随机变量X.其值域为{正反正反,反正反正,反反正正,正正反反…},一共得有8种情况。
光是取个数值也没有意义,这个取值的规律才是我们要研究的内容,这个规律就是随机变量的概率分布。
数学上,叫做随机变量的分布函数.知道了分布函数,则它取任何值和它落入某个数值区间内的概率都可以求出。
大数定理
首先,已知某个随机变量的概率分布,期望是根据分布提前计算出来的;其次,对于某个随机事件,进行重复实验,每次事件结果都是一个随机变量,重复的随机变量构成随机序列,独立同分布。随机序列的取值的均值$S_{n}=(X_{1}+X_{2}+…X_{n})/n$将依据概率收敛于X的期望。
中心极限定理
大量相互独立同分布的随机变量,其均值(或者和)的分布以正态分布为极限(意思就是当满足某些条件的时候,比如Sample Size比较大,采样次数区域无穷大的时候,就越接近正态分布)。而这个定理amazing的地方在于,无论是什么分布的随机变量,都满足这个定理。
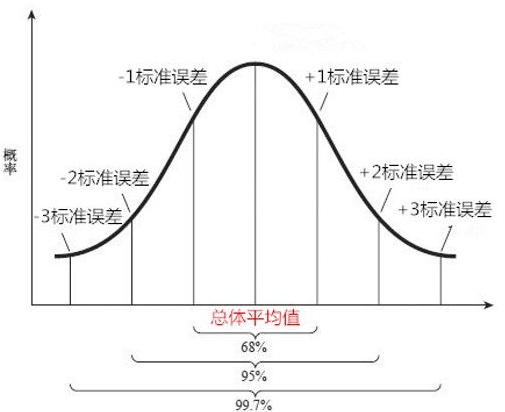
换种理解,不管什么分布,任意一个总体的多个样本的均值都会围绕在总体的平均值周围,并且呈现正态分布.多个样本的均值求得的标准差,为样本的标准误差,也可以来近似估计总体的标准差.随着样本增多,并且这个正态分布的标准差越来越小.
-
严格意义上,上面的不管什么分布是有限制的,要求$E(X^{2})< \infty$.
-
核心就是原整体的分布不重要,总是可以多个样本均值来估计原整体的均值,(方差同理?).样本足够大时,足够合理时,甚至
一个样本就够了 -
注意,并不是估计原样本本身属于正态分布,而是其样本均值的分布呈正态分布
根据样本平均值概率图,也就是置信区间的概念,还可以用来评估某个样本是否合理.
如果我们掌握了某个总体的具体信息,然后得到了某个样本的平均值,当其减去总体均值大于3个标准误差时,根据99.7%的样本平均值会处于总体平均值3个标准误差的范围内,因此我们可以得出该样本不属于总体的结论.
两者的区别理解
中心极限定理指的是样本均值的抽样分布接近于期望为u的正态分布。 大数定理指的是当样本量无穷大时,样本均值接近于总体均值u。
可以再看看这里的回答.
相关应用
-
蒙特卡洛方法
-
假设检验
异常检测算法
异常检测用来检测离群点.
假设数据集合的特征之间独立,且每个特征服从一元高斯分布.
首先记得要挑选feature,不是一股脑把所有features就拿去参数估计。

已经某些异常点了,然后分好train/cv/test 训练集用来参数估计,cv用来评估算法的好坏,标准还是要用准确率,召回率,F值,不能只看误差率。评估算法也可以用来选择$\varepsilon$.

- 为何不直接用ml学习算法来分类(y=0正常,y=1异常)?
当异常点很少(10-20个?)时,直接异常检测就好,学习算法效果不好。
-
某个特征不高斯?用直方图可看,然后用log,指数等运算让分布变得高斯。
-
增加一些特征更能表征异常
如一般情况cpu与network成正比,let x=cpu/network,可排查cpu死循环,而网络负载并不高的情况。
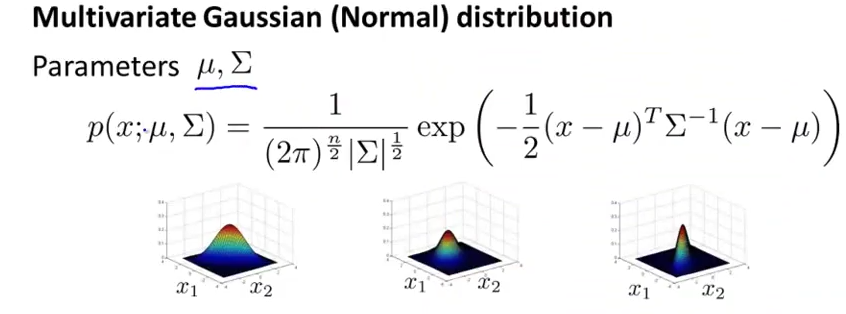
假设数据集合特征间不独立,但是整体符合多元高斯分布
多元高斯分布,$\Sigma$是特征协方差矩阵,$\mu$是特征均值向量.上面提到的多个一元高斯分布,不过是多元高斯分布的特殊情况.其协方差矩阵的非斜对角线元素均为0.
多元高斯计算代价更高.
多元高斯模型要求m>n.$\Sigma$才有逆. m»n更好.
实际中$\Sigma$的逆一般存在,若发现逆计算有问题,要看特征间是否冗余,有相等的或者有关系.或者m<n了.
算法过程:


