Machine learning Recommender system
数学补课
矩阵的秩,低秩矩阵
推荐系统
基于内容的电影推荐
电影是内容,将电影特征化,就是基于内容的实质。
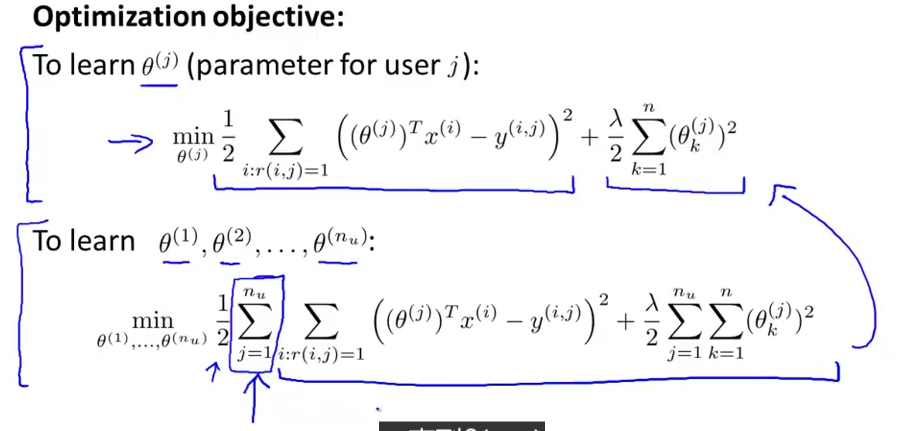
首先要清楚模型,其实对单个用户,就是要训练一个线性回归系统,y 是用户对某些电影的评分,y_predict 是没有评分过的电影,需要通过线性回归预测这些电影的评分,因此每个电影都是一个样本,有若干特征值(x0 x1 x2..).

然后再扩展到多个用户上,相当于同时算多个线性回归系统。并且代价函数合并用一个,就是要最小化这个整个系统的代价函数。
协同过滤
可以自行学习特征.
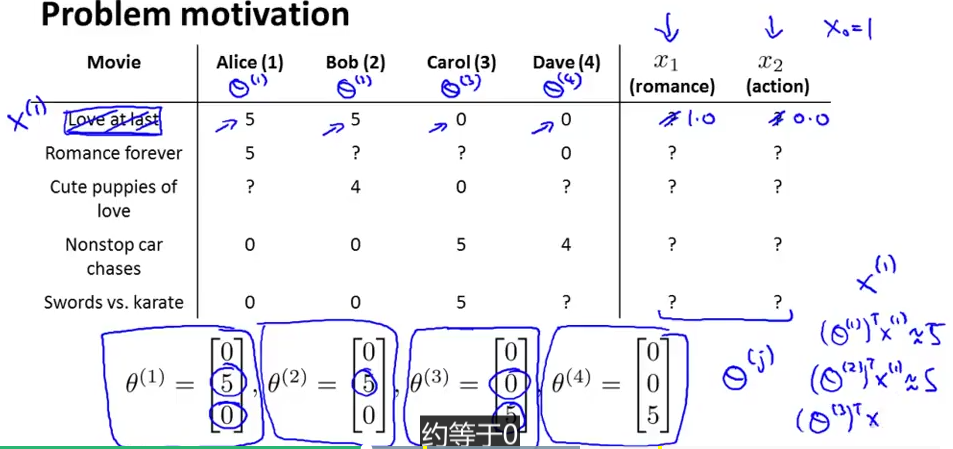
已经知道用户的电影喜好(比如上面的线性回归参数,这次可能不是算来的,是直接用户调查得到的),针对某部电影,不同用户给出不同的评分,用线性回归来预测电影的特征值.(x1 为爱情值,x2 为暴力值),还是个线性回归问题,
求解的模型变成了特征本身:
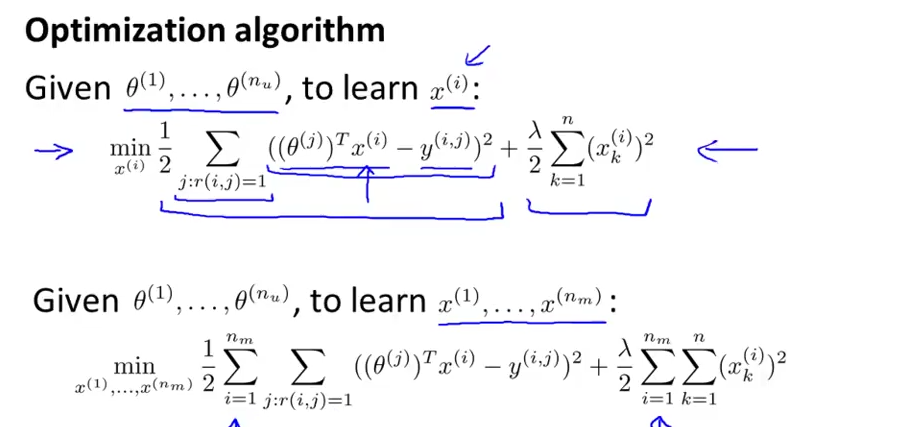
所以先学习电影特征,拿到特征后,可以预测用户评分,根据已有评分,反过来又可能学习电影特征..这就是协同的意思
协同过滤算法
将上面2个问题的代价函数再次合并为一个.同时学习特征和用户模型参数,最终直接可以预测客户对某个电影的评分

低秩矩阵分解
上面的问题经过向量化后,可以化简为矩阵的乘积:
\[Y=X\Theta^{T}\]
作业
Ng 的作业只让人实现最关键的部分,其实数据的预处理,可视化,以及思路的框架都准备好了.
- 把算法用用精确的公式表达,i,j,k 这些逻辑层次特别重要;
- 把过程分解,细化。能够像作业一样逐步验证,当然最好,效率最高。
回到推荐系统本身,如果 X 有了,theta 也有了,拿到一个新的用户:
- 算出缺失的电影评分,作为用户可能的喜爱程度;
-
找出用户已评分过的最高电影,计算哪些 xi-xj 接近的电影,推动给用户
训练时,也加入了该用户的数据.加不加应该无所谓?
num_feature=10 是怎么确定的,不能等于 9/8/7?

