Machinelearning Boosting算法深入理解
这是之前做的一个笔记
Boosting 与 Bagging 的区别
ensemble 包括 boosting,bagging,stack 等等.
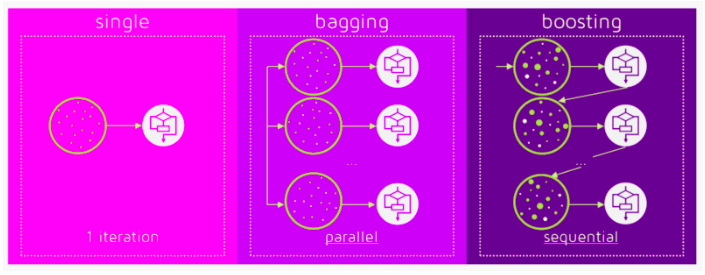
bagging 属于有放回抽样,每个弱分类器的 traning 数据不同,对树方法,可能从全部特征里,随机选部分特征。得到 n 个模型后,用weighted average, majority vote or normal average这些方法最终 ensemable 一个模型,
降低 variance,倒有点像 nn 里的drop out
常见的就是Random Forest Models
另外 bagging 的模型可以并行计算,而 boosting 依赖上一个 weak learner,只能串行.
Boosting
boosting 本身不区分回归还是分类问题,都可以使用,看具体用什么样的 weak learner + loss 函数
Adaboost
Adaboost 是最早的 boosting 算法,其核心是样本加权,然后针对分错的样本(分类)或者误差较大的样本(回归),下一个 weak learner 将重点照顾,直到把错误减小。 而且每个 weak learner 也都有个权重,最终的模型预测值为:
\[G(x) = sign(f(x))=sign(\sum_{m=1}^{M}(\alpha_{m}*G_{m}(x)))\]About weak learner
问题 1: \(G_{m}(x)\)是第 m 轮训练的 weak learner,具体如何训练,如何选择 loss function?
问题 2: 上一次分错的,权重越大。如何加权?
注意weak learner的概念,它是比随机稍微好一点的 leaner。而 Adaboost 里用的 weak learner 可以是非常简单的单层决策树,先选择特征 l,再算分类点 a,选择合适的 loss,特征分裂后,计算加权的最小错误分类率(分类)or 加权的最小平方误差(回归),就可以得到本轮的\(G_{m}(x)\)
The weak learners in AdaBoost are decision trees with a single split, called decision stumps for their shortness.
分类问题
对于分类问题,自然可以用传统分类树里的条件熵,基尼系数这些来当分裂标准(split standard).
但要注意,最终 metric 是加权后的错误率,而不是最低的 Gini or 条件熵. 而依最低 Gini or 熵找到的\((a,l)\)也许可以得到最低的加权错误率,也许也不可以.总之:
搜索\((a,l)\)的空间,每次统计按\((a,l)\)分裂 train set 后的错误分类率,再加上权重,选择最低\(e_{m}\)的\((a,l)\)作为\(G_{m}(x)\).
\[e_{m}=P(G_{m}(x)\neq y_{i})=\sum_{i=1}^{N}w_{m,i}I(G_{m}(x)\neq y_{i})\]根据\(e_{m}\)更新\(\alpha_{m}\):
\[\alpha_{m}=0.5* log(\frac{e_{m}}{1-e_{m}})\]回归问题
对于回归问题,依据 mse loss,选好\((l,a)\),重点来了,是计算每个样本带加权的 rse!
rse 越大,该回归器的权重\(\alpha_{m}\)也越大,错误样本加权的系数 w 也变大,因此最终得到的 minimum rse 是朝着最小化错误样本的误差的目标去的.
\[G_{m}(x)=arg\ \underset{l,a}{min}\ w_{i}*\sum_{i=1}^{N}\left ((y(x^{l}_{i})-y)^{2}_{i<a} + (y(x^{l}_{i})-y)^{2}_{i>=a} \right )\]进一步,如何根据 rse 来更新\(G_{m}(x)\)的权重\(\alpha_{m}\)?
(以下仅是猜测..)
weighted minimun mse 应该有一个上界,那就是不加权时的 mse!
道理很简单:
\[ax_{1}+bx{2}+c{x_3} < x_{1} + x_{2} + x_{3} , when\ a + b+ c =1\]所以有\(r_{m}\)在[0,1]之间:
\[r_{m} = \frac {r_{m, weighted}} {r_{not \ weighted}}\]再算\(\alpha_{m}\)就可以了:
\[\alpha_{m}=0.5* log(\frac{r_{m}}{1-r_{m}})\]前向分步加法模型
Adaboost 是前向分步加法(stage-wise additive model)的一种,他的特殊在于 weak learner 是加权的,adaptive 嘛.
而一般的 Additive Model 并没有考虑 weak leaner 的加权,比如下面提到的 boosting tree.
additive model 正是 Graident boosting 预测残差的基础: \(f_{m}(x)=f_{m-1}(x)+ \alpha * g_{m}\)
Boosting Tree
以决策树作为 weak learner 的提升方法为提升树, 包括了回归方法和分类方法.
这里的 weak learner,比上面 adboost 用的又要强一点,可能是一颗大树但不完全(有若干结点),下面以回归问题为例:
最终预测模型仍然是以分步前向加法模型为基础:
第 m 步前向时:
\[\vartheta_{m}=arg\ \underset{\vartheta_{m}}{min}\sum_{i=1}^{N}L(y_{i},f_{m-1}(x)+T(x_{i},\vartheta_{m}))\]weak leaner 选择回归树,损失函数为mean square error loss
r 即是上一个分类器与 y 的残差,第 m 步的回归器\(G_{m}\)针对该残差 r 进行估计即可.
求解:
\[f(x)=\sum_{m=1}^{M}C_{m}I(x\epsilon R_{m} )\]其中\(R_{1},R_{2},...R_{M}\)为回归树划分的 M 个子区域;
基于平方误差最小(mse)的规则,\(C_{m}\)为各自区域的 y 的平均值:
\[\hat{C_{m}} =ave( y_{i} | x_{i} \epsilon R_{m} )\]
Gradient boost
gradient-boosting-from-scratch
- 残差拟合
其实上面的残差就是梯度,不过因为 loss 函数是 mse,这个解简单,好算。
而Gradient boost方法就是用梯度下降法去解决这一类数值优化问题的方法,loss 函数看成是 f(x)的函数,
它要求loss函数对f(x)可导就行了。

Generally this approach is called functional gradient descent or gradient descent with functions.
对于不是 mse 的可导的 loss 函数,用最陡下降法的近似方法,取loss函数的负梯度在当前模型的取值来拟合残差,从而估计相应的 weak learner:
After calculating the loss, to perform the gradient descent procedure, we must add a tree to the model that reduces the loss (i.e. follow the gradient). We do this by parameterizing the tree, then modify the parameters of the tree and move in the right direction by (reducing the residual loss.
Generally this approach is called functional gradient descent or gradient descent with functions.
Gradient boost decision tree(GBDT)
GBDT 是 weak learner 是决策树的 Gradient boosting 算法

其中第 c 步,是预测 leaf 的分段 regresiion value,如果 loss 函数为 MSE,这个估计就是均值(mean),如果为 MAE,这估计就是中值(median)
如何实现更好的 GBDT
GBDT 容易 overfit
- Tree Constraints
少几个树模型,叶节点,大一点的特征门限
- Shrinkage
rmi 是求梯度,类似 GD,用 learning rate 控制速率,学的慢,树个数也就多了,需要 trade off
- Random sampling
A few variants of stochastic boosting that can be used:
Subsample rows before creating each tree.
Subsample columns before creating each tree
Subsample columns before considering each split.
- Penalized Learning
关于 GBDT 算法的 weak learner 的 training
仅用 1 个特征来简化问题描述
weak learner 此时是一个desicion tree stumps, 1 个特征,1 个切分点,分为 R1,R2 两个区域:
- 对 r(残差)估计
loss 选用 L2 loss or MSE(均方误差损失)时,在 GBDT 里是对 r(残差)估计,求最佳的 s:
r 包括了幅度和方向
\[s = arg\ \underset{s}{min}\left ( \sum_{x\epsilon R1}(x-c_{1})^{2}+ \sum_{x\epsilon R2}(x-c_{2})^{2}\right )\]其中
\[c_{1} = \sum_{y\epsilon R1}y;c_{2} = \sum_{y\epsilon R1}y\]实际求解时,可以列出所有的 s 和 c1,c2 的组合,可以更直观的看出哪个组合取最小的 MSE
- 对 sign(r)即残差的方向估计
另外还有 loss function 为 L1 loss,or MAE (mean absolute error)
MAE 的好处是对 outlier 不会拟合,(中值的缘故,不考虑那些最小最大值),相对 MSE,不容易 over fit
在 GBDT 里是对 sign(r)进行估计, 即对仅包括残差方向的 vector 估计:
\[y-f_{m}(x)=[-1,0,1,1]\]选择切分点 a,并且也 sign 化,即
\[\\ x=a, \ x=0; \\ x>a, \ x=1;\]将样本集x同样变成[1,-1,0,1..]这样的vector,再用MSE衡量,求得最佳的a:
这里用MSE而不是MAE,前者收敛的更快
$$
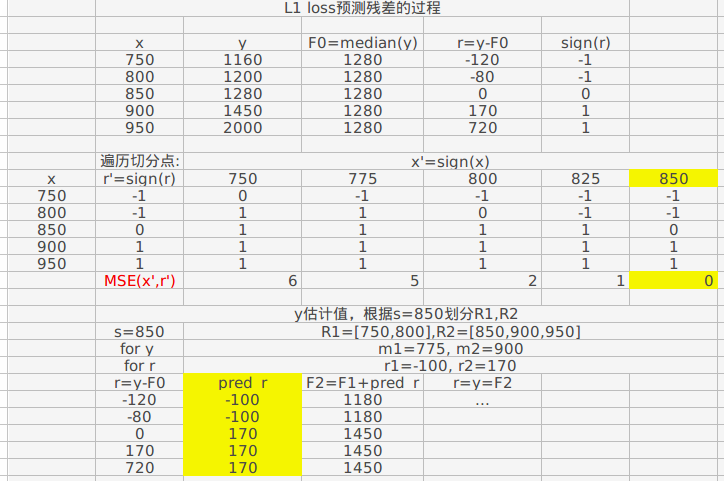
前面使用sign(r),仅仅是为了更好的划分 R1,R2,最终的目的还是要做估计,而不是分类。根据 a 划分的 R1,R2,用 median(r)来估计 y.
参考阅读
更详细的解释文中GBM optimizing MAE by example 关于 L1 loss 下 weak learner 的预测过程: