Deep learning Nerual network深入理解
注意
- 注意
Summing up, a more precise statement of the universality theorem is that neural networks with a single hidden layer can be used to approximate any continuous function to any desired precision. In this chapter we'll actually prove a slightly weaker version of this result, using two hidden layers instead of one.
神经网络模型的直观展示
立体展示 2 hidden layer 神经网络模型的工作原理
为何训练 deep nerual networks 很困难
梯度消失和爆炸
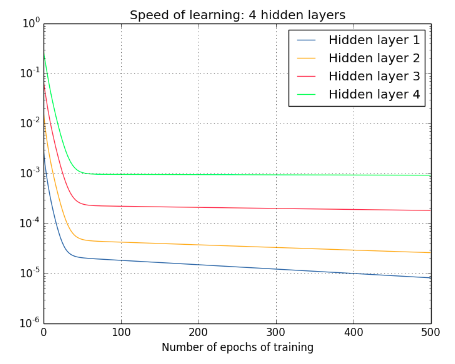
反向传播时,随着 layer 越往前,梯度也是变的越来越小。the gradient tends to get smaller as we move backward through the hidden layers.
反之则是梯度爆炸
简单的表达:

复杂的网络里(bp 算法里的推导):
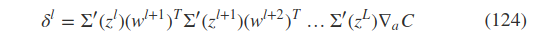
总之,这两类问题的根源是,It’s that the gradient in early layers is the product of terms from all the later layers.When there are many layers, that’s an intrinsically unstable situation.
前面的 layer 的梯度是后面 layer 梯度的乘积,后面 layer 的梯度如果变小,那前面乘积起来自然也变小,后面 layer 的梯度在增加(超过 1 的乘积),那么前面的梯度也会增大
当前的业界的解决:Relu?
初始化 weight 的选择
sigmoid as output layer
前面学习 bp 算法时,sigmoid as ouputlayer ,算梯度时,由与 sigmoild 本身的特性,求导后,接近 0 or 1 时,函数值变化变的很小,即参数学习的速率大大降低,这是另外一种梯度消失.
当前的业界的解决:softmax + log loss? or sigmoid output + cross-entry?
选择不同的 gradient descent 的困难
什么情况适应什么样的 momentum with stochastic gradient descent?
解决:fastai 里的那些技巧?

