• k-means
  • 流程
  • 技巧
• demensionality reduction(维度约减)
  • PCA 主成分分析
  • PCA 使用注意
  • 数据可视化 data visiualazation
• 一些数学知识补充

k-means

clustering 算法，无监督.

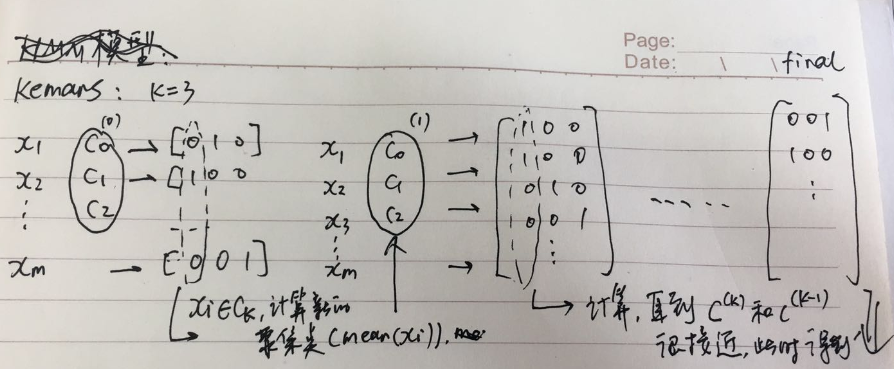
流程

1. 选择 K
2. 随机选择 k 个中心
3. 计算所有样本到每个中心的距离，距离最短的，将样本标记为第 k 类
4. 计算所有标记类的距离均值,作为新的中心点，步骤 3.直到中心点收敛。

技巧

随机初始化中心点时，不是真的随机选点，而是直接从样本里选，效果更好.

某次运算后，可能陷入局部最优,解决方法是多来几次,选择最小的(用 k-means 的代价函数(失真函数 distortion functiion))那次分类

\[J(c^{(1)},c^{(2)}...c^{(m)},\mu_{1},...\mu_{k}) = \sum_{i=1}^{m}||x_{c^{i}}-\mu_{k}||^{2}\]

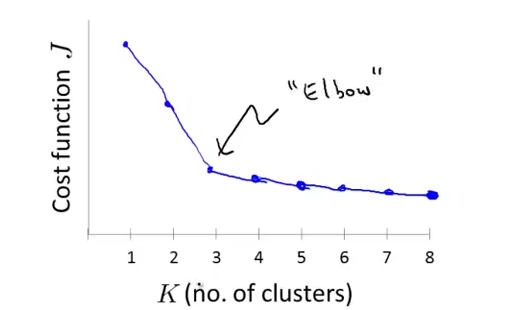
如何选择聚类的个数 K?elbow methed,同样看 distortion functiion.也不能完全保证.另外的方法是看实际效果.

demensionality reduction(维度约减)

PCA 主成分分析

从 n 维降到 k 维,核心就是奇异值分解,k 维到 n 维也可以用 Ureduce(nxk x kx1)来复原。

选择 k 的一个方法:

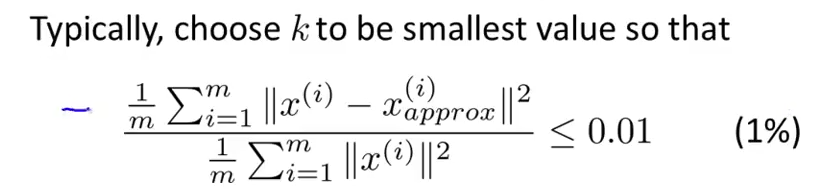
问题什么是$x_{approx}$?还是不求了，直接用奇异值:

即降维后，数据与原始数据的均方误差，应该只能占原始数据的很少比例,1%/5%/10%

疑问是，这里都是用基本协方差矩阵，而在图像压缩里，是直接将图像矩阵 svd?图像压缩把每一行看成一个特征集合(100x100,每行 100)，而图像识别这类，是把整个图像作为一个特征集(100x100,特征集是 10000x1).

PCA 使用注意

PCA 用来降维压缩存储/可视化比较好.

不应该降维后去做 ml 处理，因为实际丢失了信息，并不一定利于 ml 的学习，一定先用原始数据，如果发现算法特别慢，内存不够，可以考虑用 PCA 后评估,但仍然不推荐用 PCA 去降维度 training data.

数据可视化 data visiualazation

降维度到 2-3 维，再画出来

一些数学知识补充

• 线性相关，线性无关，秩

参考

参考

n 个向量的组(矩阵)线性无关，表示可以由这 n 个向量张成一个 n 维空间，而线性相关则是 n 个向量里，可能只有 m 个可能张成一个 m 维空间，其中有的向量可以用其他向量的线性组合来表达，m<n.m 即是秩

把秩比喻成一组向量“干货”的多少，一组向量线性相关表示有一个向量能被其他向量的线性组合表示出来，说明它是“水分”.

对于向量空间，这一组向量为基向量，该空间的向量都可以用一组基向量的线性组合来表达，但是基向量并不唯一.

• 向量的内积

\[u^{T}v=||v||*||u||cos(\theta)=u_{1}*v_{1}+u{2}*v_{2}\]

表示向量 u 在 v 上的投影$||u||*cos$ 与 $||v||$的乘积,如果矩阵化，即:

\[y=U*v\]

表示 v 在一组向量矩阵上的投影，该向量可以为规范正交基,U 为投影矩阵.

• 正交矩阵

矩阵向量的任意向量内积内 0，即相互垂直，如果$||u||=1$ ，则是向量是一组标准正交基,这样的矩阵叫做标准正交矩阵,正交矩阵有性质:

\[AA^{-1}=AA^{T}=I\ ,\ A^{T}=A^{-1}\]

• 正定矩阵

对任意矩阵 M,$x^{T}Mx\geq0$,则 M 是正定 or 半正定的(取等号),$y=Mx$表对向量做几何变换,而$x^{T}y$结合上面内积的意义，表示向量 x 在经过 M 的变换后，同原 x 有了夹角，该夹角的度数应该小于等于 90°.

• 对称矩阵

这个比较简单，$A=A^{T}$

• 奇异值分解

• 协方差矩阵

描述的是样本的特征(n)之间的相关性，而跟样本数无关，X’*X 为 nxmxmxn=nxn 维，即只有 n 的参与。

首先 PAC 需要以中心化了的$X$的协方差矩阵为计算,意味着$E(x)=0$,PCA 的目标是(n 维降到 k 维,kxn x nxk = kxn)

协方差矩阵是一个对称正定矩阵

\[st. W^{T}W=I\]